Técnicas de reducción de dimensionalidad

Entendiendo el contexto

En la actualidad, en la mayoría de los problemas de ciencia de datos, el conjunto de datos está sobrecargado con numerosas características que dan como resultado un sobreajuste y además aumentan los enormes costes computacionales, lo que hace que el proceso sea considerablemente lento, y esta no es la excepción, una de las soluciones a este problema es reducir la dimensión del conjunto de datos.

El principal objetivo de este trabajo es analizar qué tan factible es ocupar algunas técnicas de reducción en el conjunto de datos y la razón de por qué algunas funcionan mejor que otras en este conjunto, además de presentar los resultados obtenidos en los distintos experimentos comparando su eficiencia.

Por ello, en este trabajo se lleva a cabo el estudio de algunas técnicas de reducción de dimensionalidad, las matemáticas tras estas, las ventajas y desventajas de cada una, que librerías utilizan y cómo se aplican al conjunto de datos, también se verán los inconvenientes que presentan los algoritmos de aprendizaje automático en problemas con estas características.

Posteriormente, se lleva a cabo el estudio empírico del análisis discriminante lineal (LDA), como su nombre lo indica, el análisis discriminante identifica las características que diferencian a dos o más grupos y a crear una función capaz de distinguir con la mayor precisión posible a los miembros de un grupo u otro. Por otro lado, LDA también es un método de reducción de dimensión, dado que su objetivo es proyectar el espacio de una característica (conjunto de datos n-dimensional) en un subespacio pequeño k donde k n – 1, manteniendo la información discriminatoria de clases.

Luego, se muestra una comparación de los resultados obtenidos con PCA, la técnica estadística más tradicional y conocida que existe. Esta técnica lleva a cabo la transformación de los datos generando nuevas componentes, conocidas como componentes principales, que se calculan teniendo en cuenta la varianza del conjunto de datos. El primer componente principal es definido por el método donde el conjunto de datos presenta una mayor varianza, el segundo componente principal es definido donde los datos presentan la segunda mayor varianza, y así sucesivamente.

Hay que tener en cuenta que el número máximo de componentes principales que se obtienen mediante PCA siempre será igual al número de variables del conjunto de datos, aunque como el objetivo es reducir la dimensionalidad habrá que reducir el número de componentes seleccionando aquellos que expliquen la mayor cantidad de variabilidad de los datos. Sin embargo, PCA presenta el principal problema, que es una técnica no supervisada, es decir, no utiliza el valor que se espera obtener para cada dato. Por este motivo, PCA puede proporcionar resultados no satisfactorios. Para hacer una evaluación de la calidad de la reducción de la dimensionalidad producida, en ambos casos, se utilizan distintos algoritmos de clasificación, estos son: K-nearest neighbors (KNN), Regresión logística y Redes neuronales.

Primero, se utilizarán estos algoritmos para clasificar los datos sin haber realizado ninguna reducción de dimensión, y así poder ver qué resultados se obtienen antes de la investigación. Estos resultados se muestran en la Tabla 1.

MÉTODO	TASA MEDIA DE ACIERTO
Regresión logística	61.7%
K vecinos más cercanos	53.9%
Redes neuronales	44.3%

Tabla 1. Exactitud de los distintos métodos de clasificación sin aplicar técnicas de reducción de dimensión.

Comparación de distintas técnicas de reducción de dimensionalidad

A continuación, para comparar distintas técnicas de reducción de dimensionalidad, se muestra una tabla con las ventajas y desventajas que pueden implicar las distintas técnicas.

Método de reducción	Ventajas	Desventajas
Análisis de componentes principales (PCA)	Retiene las características del conjunto de datos que contribuyen más a su varianza. Se ejecuta bastante rápido a comparación de otras técnicas como t-SNE. Después de la transformación conserva la varianza en los datos, usando valores propios.	No ofrece resultados satisfactorios en muchos problemas supervisados de clasificación o regresión al tratarse de una técnica no supervisada. Las nuevas coordenadas ya no son variables reales producidas por el sistema, por lo que la aplicación del PCA al conjunto de datos hace que se pierda capacidad de interpretación. Muy influenciado por los outliers en los datos, por lo que es recomendable estudiar si los hay.
Análisis de discriminante lineal (LDA)	Al igual que PCA se ejecuta bastante fácil y rápido.	La clasificación de nuevas observaciones no es muy eficiente a medida que se incrementa el número de variables en el modelo. Se acostumbra a hacer selección de variables antes de aplicar el método. Requiere que se especifiquen los grupos del conjunto de entrenamiento del modelo con clases prefijadas.
Análisis factorial	Ayuda a simplificar la información que nos da una matriz de correlaciones para hacerla más fácilmente interpretable.
Incrustación de vecinos estocásticos distribuidos en t (t-SNE)	Se suele utilizar para la reducción de dimensionalidad no lineal y la visualización de datos. Mantiene los puntos de datos muy similares juntos en el espacio de menor dimensionalidad. Los valores atípicos no afectan a t-SNE.	Realiza una cantidad enorme de cálculos, lo que se traduce en un proceso muy lento cuando se trabaja con varios miles de observaciones. Está diseñado para reducir los datos a 2 o 3 dimensiones. No debe aplicarse si la reducción de dimensionalidad se hace a espacios d > 3. No es un proceso totalmente determinista, por lo que, a pesar de emplear los mismos datos, los resultados pueden variar. Su algoritmo no es incremental, en otras palabras, no puede aplicarse sobre un set de datos y después actualizarlo con unas pocas observaciones nuevas. Se tiene que ejecutar de nuevo todo el algoritmo incluyendo todas las observaciones (las viejas y las nuevas).

Tabla 2. Ventajas y desventajas de las técnicas de reducción de variables.

Construcción del conjunto de datos final

Para construir el conjunto de datos final se realiza una reducción de variables al conjunto de datos inicial, como ya vimos existen distintas técnicas para realizar esta reducción, en este trabajo se prueban 3, estas son PCA, t-SNE y LDA.

Donde, con la ayuda de la tabla 2, se decide que de entre las vistas LDA es la técnica más adecuada y con la que a su vez se obtendrán mejores resultados, ya que PCA al ser una técnica no supervisada y también ser muy sensible a los outliers no ofrece tan buenos resultados y con t-SNE se obtienen muy malos resultados ya que esta es una técnica no supervisada y más enfocada en la visualización de los datos que en la clasificación.

Por otro lado, LDA a diferencia de PCA y t-SNE es una técnica supervisada y además no es tan sensible a los outliers como PCA. Para comprobarlo, se clasificará el modelo tras aplicar cada una de estas técnicas de reducción, los algoritmos de clasificación que se utilizarán para esto son K-nearest neighbors (KNN), Regresión logística y Redes neuronales.

Se realizará una tabla que contendrá el algoritmo utilizado y el porcentaje de acierto que se tuvo tras aplicarlo. Se comenzó probando con PCA, donde primero se realizó un estudio para determinar la cantidad de componentes principales a las que será reducida la dimensión inicial, acá se obtuvo que con un total de 40 variables se logra explicar un 85% de la información de estos, lo que es bastante bueno, por lo tanto al utilizar PCA se reducirá la dimensión a 40.

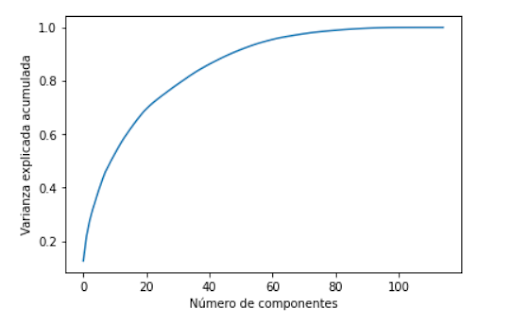
Figura 1. Número de componentes principales v/s varianza explicada acumulada.

Clasificación con PCA

Como ya se mencionó anteriormente, se realiza una reducción de variables con PCA, donde se reduce a una cantidad de 40 componentes principales, los resultados son presentados en la siguiente tabla:

Método	Tasa media de acierto
Regresión logística	69.6%
K vecinos más cercanos	64%
Redes neuronales	66.4%

Tabla 3. Exactitud de los distintos métodos de clasificación tras realizar una reducción de dimensión a 40 componentes con la técnica PCA.

Clasificación con t-SNE

Ahora, se realiza una reducción de variables con t-SNE, los resultados obtenidos son los siguientes:

MÉTODO	TASA MEDIA DE ACIERTO
Regresión logística	69.6%
K vecinos más cercanos	64%
Redes neuronales	66.4%

Tabla 4. Exactitud de los distintos métodos de clasificación tras realizar una reducción de dimensión con la técnica t-SNE.

Clasificación con LDA

Y por último se verán los resultados que se obtuvieron con LDA, que como se analizó anteriormente, es la técnica más adecuada y con la que a su vez se obtendrán mejores resultados entre las técnicas aplicadas.

MÉTODO	TASA MEDIA DE ACIERTO
Regresión logística	69.6%
K vecinos más cercanos	64%
Redes neuronales	66.4%

Tabla 5. Exactitud de los distintos métodos de clasificación tras realizar una reducción de dimensión con la técnica LDA.

En la tabla 5, se puede apreciar que con todos los métodos se logró una tasa media de acierto bastante parecida, pero con el método que mejor se clasificaron los datos fue con el de los K vecinos más cercanos, con un total del 70,5% de los datos clasificados correctamente.

Como con esta técnica se obtuvieron los mejores resultados, por lo que se hará un análisis más detallado en su comportamiento, para esto se realiza la matriz de confusión para cada uno de estos métodos de clasificación, así se va a observar qué tan bien clasifica a las distintas clases cada uno de estos métodos.

Tabla 4. Exactitud de los distintos métodos de clasificación tras realizar una reducción de dimensión con la técnica t-SNE.

Resultados LDA

TASA MEDIA DE ACIERTO
Target	Regresión logística	K vecinos más cercanos	Redes Neuronales
0	69,4%	69,7%	70,8%
1	61%	61,5%	59,7%
2	76,4%	82%	78,3%
3	79,5%	74,9%	76,7%

Tabla 6. Exactitud en cada una de las clases con todos los métodos utilizados anteriormente .

En la tabla 6 se puede ver que el método que mejor clasifica la clase “0” es el de Redes Neuronales, el que mejor clasifica la clase “1” es el de los K vecinos más cercanos, con respecto a la clase “2” el que mejor lo clasifica es nuevamente el método de K vecinos más cercanos y por último el que me mejor clasifica la clase “3” es Regresión logística.

Al ver los resultados obtenidos en la Tabla 1 y compararlos con los obtenidos tras aplicar LDA (Tabla 5) se puede ver que hubo una gran mejora en la exactitud de la clasificación en todos los algoritmos.

En esta investigación han habido varias opciones de métodos de reducción de dimensión que no se han alcanzado a explorar y aplicar, por lo tanto una línea que queda por realizar es hacer la misma evaluación con los distintos algoritmos de clasificación pero utilizando otras técnicas de reducción de variables, con los que se podrían obtener mejores resultados a los ya se obtuvieron.

Table of Contents